Somos una raza con suerte. De las infinitas posibilidades de las infinitas decisiones a las que seguramente fuimos sometidos muchas veces, fuimos la que con una serie de fortuitos accidentes convergió hasta lo que somos hoy en día. Desde el primer neandertal que, solo la tierra sabrá cómo, descubrió el fuego hasta las brillantes mentes e ideas que aun hoy, son los custodios de la luz que ilumina nuestro universo. Somos el punto culminante de miles de resultados previos. ¿Como seria el mundo si Newton hubiese sido soldado? ¿Si Einstein hubiese sido el líder del Tercer Reich? ¿Si Arquímedes hubiese sido un tirano de la antigua Grecia? Seguramente, tan diferente seria el mundo que no tenemos una imagen representativa de tal momento; nuestras mas recónditas pesadillas no se asemejarían a tal mundo, o bien puede ser que sea exactamente igual a la actualidad. Pero ¿Por qué estas personas fueron tan importantes? De seguro Newton no fue el primer ser humano al que se le cayó una manzana en la cabeza; Arquímedes no fue el primero en meterse en una bañera. Seguramente no fueron los primeros, pero si fueron los únicos que cayeron en la cuenta de cosas que nadie antes se había detenido a pensar y meditar. Cosas que ante los ojos románticos de los que ignoran su realidad pasan desapercibidos, pero que ante de los ojos de un matemático, un químico, un físico, son marcas maravillosas de la magnificencia de un mundo que hasta hoy en día, tratamos de descubrir, y mas grande aun, de entender.
No es un secreto que las matemáticas pueden ser un dolor de cabeza para muchos, pero hay un problema, que aun cuando su dificultad no deja de ser elevada en cierto grado, es capaz de atraer a las mentes mas juguetonas, sin mencionar que es la base de casi todos los problemas que se ven en física en el colegio, pero que nunca se estudió a fondo; solo se resignaron a darnos unas formulas y a aprendérnosla como el todo buen niño. pero que si las vemos hace 200 años, veremos que son o fueron el resultado de dolores de cabeza para grandes físicos como Newton, el cual no lograba comprender por que la luna no estaba donde el predecía que debía de estar. Este fue conocido como “El Problema de los 2 Cuerpos”
El problema de los 2 cuerpos
El problema es el siguiente: “Dadas 2 partículas (o cuerpos perfectamente esféricos con distribución y densidad uniforme en su interior o también cuya densidad sea solo función de la distancia) de masas m1
y m2
completamente aisladas de las demás masa que conforman El Universo, encontrar el estado dinámico de ambos cuerpos con respecto a un sistema inercial dado, cuando las únicas fuerzas que se efectúan sobre ellos son las de atracción newtoniana”. Siguiendo este orden de ideas, el problema nos plantea 3 grandes retos que fluyen de uno a otro.
1. Hallar las ecuaciones diferenciales que gobiernan el movimiento de las partículas con respecto a un sistema inercial dado.
2. Habiendo hallado las ecuaciones diferenciales que describen el movimiento del sistema, tratar de resolver la mayor cantidad posible de ecuaciones diferenciales del movimiento, para así saber las cantidades que se conservan o no se conservan, que tipo de trayectoria describen los cuerpos y bajo que circunstancias preservan ciertas simetrías.
3. Con las cantidades conservadas (Constantes) que resultan de integrar las ecuaciones diferenciales, hallar el vector de posición y velocidad para cualquier tiempo que se desee.
Ahora, ¿Por que este problema es tan asombroso? La razón es que aun si en el papel es fácilmente demostrable, en la vida real existen variables y perturbaciones que hacen que no se permita ver y dimensionar tales resultados. Para ello existen ciertos problemas que son más amplios y que permiten estudiar este tipo de variables, pero que no profundizaremos en este artículo. Cuando digo “en la vida real” y cuñado hablo de variables y perturbaciones, me refiero a ciertas características que posee el sistema que se salen del marco que se esta analizando, como lo seria un objeto que no es totalmente esférico, como el caso de un cometa, o si entran en juego fuerzas externas, como un tercer cuerpo que perturba gravitacionalmente a los otros 2, o las interacciones de campo magnético.
Ahora, existen 2 maneras de ver dicho problema. La primera forma es analizando el sistema desde su centro de masas. Esto quiere decir que nos vamos a salir de ambas masas, y veremos como se mueven, como si nosotros no estuviéramos allí. Esto implica fijarse un punto entre m1 y m2 donde ambos cuerpos se hallen en equilibrio total y ver como cambia todo el sistema a medida de que los 2 cuerpos interactúan entre si. Es fascinante de ver, ya que se logra identificar el cambio que ambas masas lleguen a tener a medida que el tiempo transcurre. Esta labor es bastante extenuante, pué implica conocer de manera previa la distancia entre el observador y el centro de masas del sistema, las magnitudes de ambas masas y la distancia entre los centros de ambas partículas hasta el centro de masas del sistema. Con estos datos podemos conocer el vector de posición de ambas masas con respecto al observador
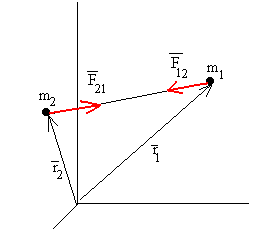
Con solo esta información ya podemos ver la descripción del movimiento en coordenadas esféricas, en función del tiempo. Hay otro sistema mucho más sencillo de analizar, pero no tan bello como el anterior. Este es el problema visto desde una de las dos masas como si esta fuera el observador o si el observador estuviese dentro de la masa central. El problema se reduce a la mitad; solo hay que saber las magnitudes de las masas, loa velocidad del segundo cuerpo y el vector de posición de el segundo cuerpo. Para poder analizar mejor este problema, con los parámetros anteriormente dichos, se deberá tener presente que la relación entre distancia y velocidad, permite deducir el momento angular, la cual siempre es una constante, por que esta magnitud siempre se conserva. Esto nos permite a los observadores, estudiar la dirección y el sentido de la trayectoria del segundo cuerpo. Cuando el momento angular es igual a cero la trayectoria del segundo cuerpo será rectilínea, puesto que si es igual a cero, o la velocidad es también igual a cero ó la dirección de la velocidad es igual u opuesta al vector de posición. En estos casos la trayectoria es rectilínea. Un caso muy extraño de ver en El Universo, pero que se da. Es otra cosa muy diferente si por en cambio, el momento angular es diferente de 0. Allí podemos afirmar que la trayectoria del cuerpo describe una orbita cónica. Tras una labor monumental de algebra y calculo, es posible traducir la primera ley de repeler y generalizarla, no solo a elipses, sino al resto de secciones cónicas. A final, solo se reduce a conocer un vector de posición y la anomalía verdadera del segundo cuerpo.
Adicional mente este problema nos permite analizar la energía que posee su sistema solo conociendo la relación de energía potencial y energía cinética, que se traduciría a la energía total del sistema. Para ello solo se requiere conocer la masa y la distancia, para el caso de la energía potencial, y la velocidad del segundo cuerpo, para la energía cinética. Como podemos ver, se puede hacer casi de todo conociendo solo estos 3 valores. Inclusive, gracias a este problema se es posible hallar la masa de un cuerpo, lógicamente cuando solo se conoce la velocidad y la distancia. Para ello, el segundo cuerpo debe de ser de masa despreciable en relación al primer cuerpo, se debe de conocer el periodo orbital (velocidad) y su distancia media al primer cuerpo (distancia). Si por el contrario se desea hallar la velocidad, solo debemos remplazar los valores de la energía total del sistema y despejar la velocidad, en cada tipo de órbita.

Parece sencillo explicado así, en una era de súper computadores que procesan lo que desees y se ahorran la vasta tarea de pensar lo que tienes que hacer. Por esa razón solo detengámonos un segundo a pensar como lo hicieron estos grandes genios, los cuales, como dije al principio, solo se pusieron a meditar lo que iba mas allá de lo que estaba ante sus ojos, que solo contaban con un papel y con su ingenio, y de ese modo preguntarse el como y el porque de todo, y así, poder dejarnos un legado. Su tarea fue abismal, ya que en una época llena de mitos ¿como le explicas a los demás que te crean si no puedes demostrar en la vida real lo que estas diciendo? tal vez la razón de su gran genio, fue que algún día tal vez un niño o tal vez un escéptico les pregunto el por que de las cosas que desconocían, y en lugar de huir, buscaron hasta hallar la respuesta, aun si sus conclusiones solo llegaron a la única respuesta posible: “No sé... Pero algún día alguien si lo sabrá”.







